トレミー の 定理 - トレミーの定理の応用例
トレミーの定理の証明~3~
例えば、透明な球体の代わりに、上下の不要な部分を切り落とした形状のものでも問題ないとした。
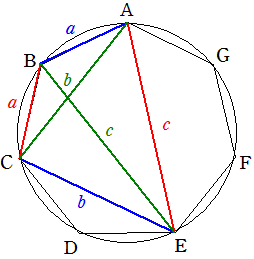
例 正七角形 正七角形の頂点を0,1,2,3,4, 5,6とする。
そして、アリストテレスの自然学と結びついて、中世のアラビア語圏や13世紀以降の中世ラテン語圏で受け入れられた。
周転円の中心は、従円 大きい円 に沿って動く。
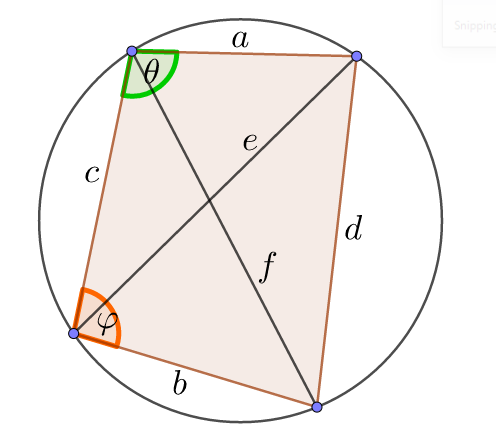
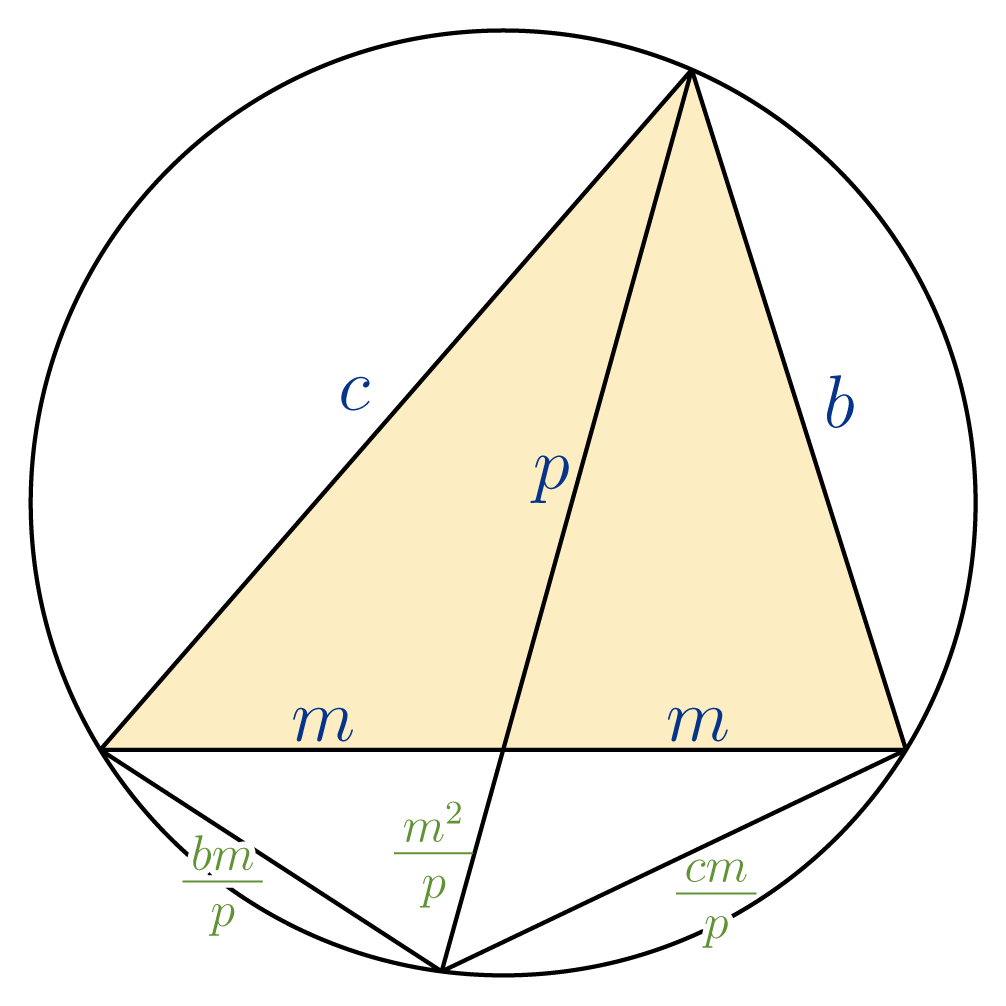
トレミーの定理
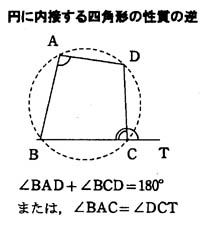
また逆に,凸四辺形 ABCDにおいて上の関係式が成り立てば,この四辺形は円に内接する。
その四角形が円に内接していれば、トレミーの定理を使うことができる。
センター対策を含め 充実のラインナップ いつでもどこでも Internetに接続された パソコンさえあれば どこでも最新の 学習履歴で学べます。
さらに、大気層の上部の屈折で星の見かけの方向が真の方向からわずかにずれることにも触れている。
三角関数の加法定理
この知識は、イベリア半島内で作成された殆どの地理データ表に反映された。
プトレマイオス世界図 大航海時代への序章. これは正攻法で得られた方程式と同じであるから、 ・・・(答) 生徒のその発見に、なるほどと膝を打った。
答えだけ知りたいのであれば、トレミーの定理を用いたほうがより簡潔に解答できます。
を手にするとをかぶりを手にするプトレマイオス。
トレミーの定理とその証明。向かい合う2組の辺と対角線の関係性|アタリマエ!
この問題は「の分割」と呼ばれ、という四弦琴の内側の二弦を調律する際に重要な問題であった。
例えば、二次関数に正確に乗っている。
Neugebauer, O. 詳細はの ページをどうぞ。
主著『』は、天体の軌道の幾何学的な理論が主な内容だが、天文学の方法論、観測、時間の決定、理論に現れるパラメータの決定、必要な数学の説明、簡単な宇宙論の概要など、天文学に関わる様々な側面を秩序だって説いている。
トレミーの定理とその証明。向かい合う2組の辺と対角線の関係性|アタリマエ!
その上で調和音程をどのように定めるかというピュタゴラス以後、古代ギリシア世界で考えられてきた問題を論じる。
黄経の理論においてはに基づく説明を用いた。
古代から中世を通じて、多くの批判や修正はなされたが、天文学の最も重要な著作であり続けた。
出差とよばれる、主に太陽の重力の効果による円運動からのずれも説明できた。
トレミーの定理とその証明。向かい合う2組の辺と対角線の関係性|アタリマエ!
円運動に基づき、地球中心で天を球体としている点はエウドクソスと同様だったが、より技巧的な仕組みを導入した。
本書には本書には、緯度の測定方法などの測量に関する理論、球面を平面に投影して図示する様々な方法が説明され、地球の(子午線一度分の長さ)や各地点の緯度や経度といったデータが収められている。
また、バビロニア由来の天文定数は古代ギリシャ天文学にも引き継がれる。
プトレマイオスの時代から見て500年前の説であるが、『ハルモニア論』によると徐々に紀元2世紀頃のアレクサンドリアの若い世代に広まっていたとされる。
中学生ができるトレミーの定理の証明方法
でも長くなってしまうので、ここからはトレミーの定理で片付けてしまいましょう。
『古代音楽論集』訳、〈〉、2008年5月15日。
ただし、科学史家カッツは、一般論として、プトレマイオスなどの建設から数百年たった後の数学者たちの場合、ギリシア系であるか否かは断定しがたいと述べている。
に二通りの証明を記載しています。
トレミーの定理の応用例
ただし、イブン・ハイサムが光を視覚の主要因と特定して光学を大きく書き換えたため、この後はイスラム圏においてもラテン西欧においても、直接の影響は限定的である。
しかしながら、現伝する筆写本は中途半端なところで切れており、これについてはテキストが散佚したと見る説と、未完成であると見る説とがある。
光と視覚の関係が明らかにされてそれらの研究が統合されるのは、中世に入ってのことである。
余弦定理などを使えば、手間は増えるものの問題なく解くことができます。
- 関連記事
2021 tmh.io