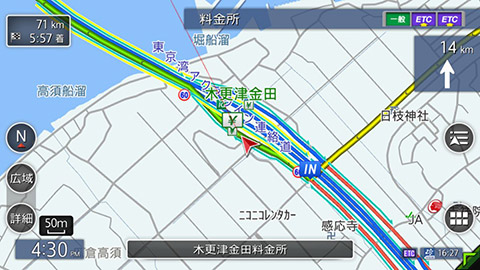
リーマン 幾何 学 - 「リーマン幾何学(裳華房)」の評価と使い方
リーマン多様体
by Karsten Grove• Sergey Brin and Lawrence Page 1998• 二乗したら-1になる数を虚数単位「i」として、2つの実数の組み合わせで表されます。
Ryuji Maehara 1984• 一般相対性理論の測地線の方程式はリーマン幾何学をまさに使っています。
可微分多様体の各点における接空間に内積を対応させる可微分写像を計量という。
齋藤 正彦 著 東京大学出版会 | 東京大学出版会• 球面および双曲空間におけるリーマン幾何学がにほかならない。
「リーマン幾何学(裳華房)」の評価と使い方
Lebesgue 1901• Trudinger• そして ,その本当の意味を知りたければ ,やっぱりリーマン幾何学を学ぶ必要があるのであるが ,パズルを解くように間を埋めていけばいいのである. このことを説明する以下の文献は秀逸です。
宇宙空間は曲がっている!? 宇宙というと平らな空間がどこまでも広がっているというイメージがありますが、アインシュタインの一般相対性理論によると、実は時空はぐにゃぐにゃと曲がっているのです。
このことは、一般的なテンソルに対しても言える。
一つの方向を含み互いに直交するすべての断面に関する断面曲率の平均をリッチ曲率といい、リッチ曲率が一定であるようなリーマン多様体を空間という。
Riemannian geometry
ラッセル自身も、自分の理論が現実の世界で「役に立つ」とは全く思っていなかったでしょう。
中内 伸光 著• 相対性理論を勉強すればするほど「リーマン幾何学をきちんと勉強していないとわかったことにならないのではないか?」と考えてしまいます。
そして、個人にとってもやはり「勉強すること」の意義の一つは「世界を広げようとすること」だと言えるでしょう。
を参照。
夢ナビ 大学教授がキミを学問の世界へナビゲート
球面の測地線は 大円コース以外にはありえない。
ニュートンが微分法を作ったのは、力学の運動法則を記述し、物体の運動の予測を行うためでした。
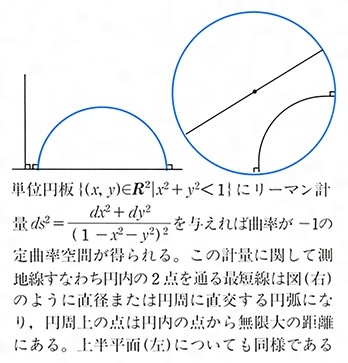
斜交座標を例に, 計量についてのイメージを理解する。
。
型理論、リーマン幾何学、四元数……かつて「役に立たなかった」数学理論たち
Gallot, Sylvestre; Hulin, Dominique; Lafontaine, Jacques 2004 , Riemannian geometry, Universitext 3rd ed. 断面曲率が一定であるようなリーマン多様体を定曲率空間という。
下図の(a)のばあいがそれです。
対称空間には等長変換群が推移的に作用しているからである。
その量を評価するには 曲率テンソルを利用します。
幾何学のすすめ
ここでa,bなどは ベクトルの番号を、i,j,k,・・・などは ベクトルの反変成分を表す指標である。
「役に立つかどうか分からない」ということ これら3つの理論はどれも、作られた当時に「この理論がこんな風に役に立つ」と予想するのは不可能だったでしょう。
リーマン幾何学をやっている途中でつらいのは ,自分が全体から見て今どれくらいの地点にいて ,どこまでやったら相対論の話題にたどり着けるのかが分からないということである. Geometry 微分幾何学(大学院)・ 幾何学XD(学部) 月曜日10:40 -- 12:10 担当:河野俊丈 講義概要: 微分幾何学に関する入門講義.多様体上のリーマン計量,接続,曲率などの基礎的な概念 とその応用について解説する. 内容:以下の項目について講義する予定である. 1. Kervaire 1960• 齋藤 正彦 訳 東京図書 | Michael Spivak• Parkin 1966• Harry Furstenberg 1955• Michael Hartley Freedman 1982• 微分幾何学は歴史的にも理論物理学と相互に影響を与えながら発展してきました。
特に物理系の方は注意。
型理論、リーマン幾何学、四元数……かつて「役に立たなかった」数学理論たち
The of a compact Riemannian manifold with negative Ricci curvature is. by Brian H. Jonathan Lewin 1991• 第4章: 絶対微分 曲がった空間におけるベクトルの微分を取り扱います。
Dmitri Burago, Yuri Burago and Sergei Ivanov• 性質 [ ] リーマン多様体において、測地的なコンパクト性やのコンパクト性、距離のコンパクト性というのは同義であり、Hopf-Rinowの定理を示唆するものである。
See also [ ]• この計量を持った R n は次元 n の と呼ばれ、 g ij can は(標準) と呼ばれる。
そのテンソルを縮約し, リッチのテンソル, スカラ曲率が定義できます。
- 関連記事
2021 tmh.io