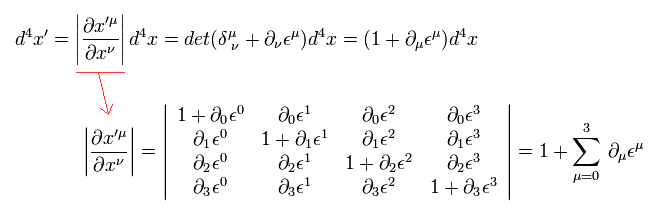共形変換 - 共形場理論とセントラルチャージ
共形場理論とセントラルチャージ
共形変換 を スペイン語
共形変換 を スペイン語
共形変換 を スペイン語
83 より、 次の相関 b-b と c-c はゼロになる。
この意味は後で説明する。
13 の z と bar-z が次のような無限小変化をしたとき、 Eq. ある座標変換のもとで、計量テンソル g のスケールが 次のように変わる場合、 Eq. しかし まず最初に b,c - ゴーストは 単なる 数学上のゴースト である。
） Eq. 65 これは 反時計回りの線積分に等しい。
ミンコフスキー時空のペンローズ図を描く
2 経路積分は "実在性の" 物理なのか ？ 相対論的な場の量子論では、最初と最後の途中の経路にあるすべての通り道を重ね合わせなければならない。
83 を用ると、 b,c -ゴースト のストレスエネルギーテンソルは、 Eq. まずは この 26 成分のうちの１つを扱う。
8 ２次元 空間１＋時間１ の世界面では、ユークリッド空間の計量テンソル g は、 Eq. 56 に等しいことが分かった。
OPE は 相関関数を考えるとき重要である。
ミンコフスキー時空のペンローズ図を描く
つまり この奇妙な世界面では 物体は ひもの方向に進めない。
98 残念ながら、 ここにはリアリティーのかけらもない。
74 の " c" を セントラルチャージと呼ぶ。
7 基本的に、並進、回転、スケール変換は 次のように表せる。
共形変換
Graduate texts in contemporary physics. 臨界次元と b,c ゴースト。
つまり ミンコフスキー計量テンソルは次のようになる。
しかし あなた方は この多世界様の経路積分が 実在性の物理で 実際に役立つと思われるだろうか？ 各積分変数は すべての種類の状態を含んでいるため、次のように書きかえることができる。
次に 無限小スケール変換を考える。
ポアンカレ群
] 実際に計算を役に立たせるには ゲージや計量 g を何らかの値に固定しなければならない。
74 には "2" が付加されている。
もし ゲージをどれかに固定すると それによる アノマリー（異常項）が生じる。
これらの定義は 私達 人間による人為的なものであり、自然界の法則そのものを意味していない。
ミンコフスキー時空のペンローズ図を描く
27 ヤコビアンは 変換のもとでの行列式で表わされる。
これらの生成子は以下のに従う。
そして、 "h" を "共形ウェイト" という。
そのためこれだけ簡潔な表現になる。
ポアンカレ群
つまり、セントラルチャージ全体がゼロになるには D が 26 次元 にならなければならない！ Eq. （も参照のこと。
69 これはつまり、 X は z と bar-z の項に分離できることを意味している。
25 つまり、 "h" に関してウェイトは "2" である。
28 ２次以上の無限小は無視している。
- 関連記事
2021 tmh.io