狭義 単調 増加 - 「狭義単調増加」に関するQ＆A

証明 1. 今回は単調増加・減少について扱いました。

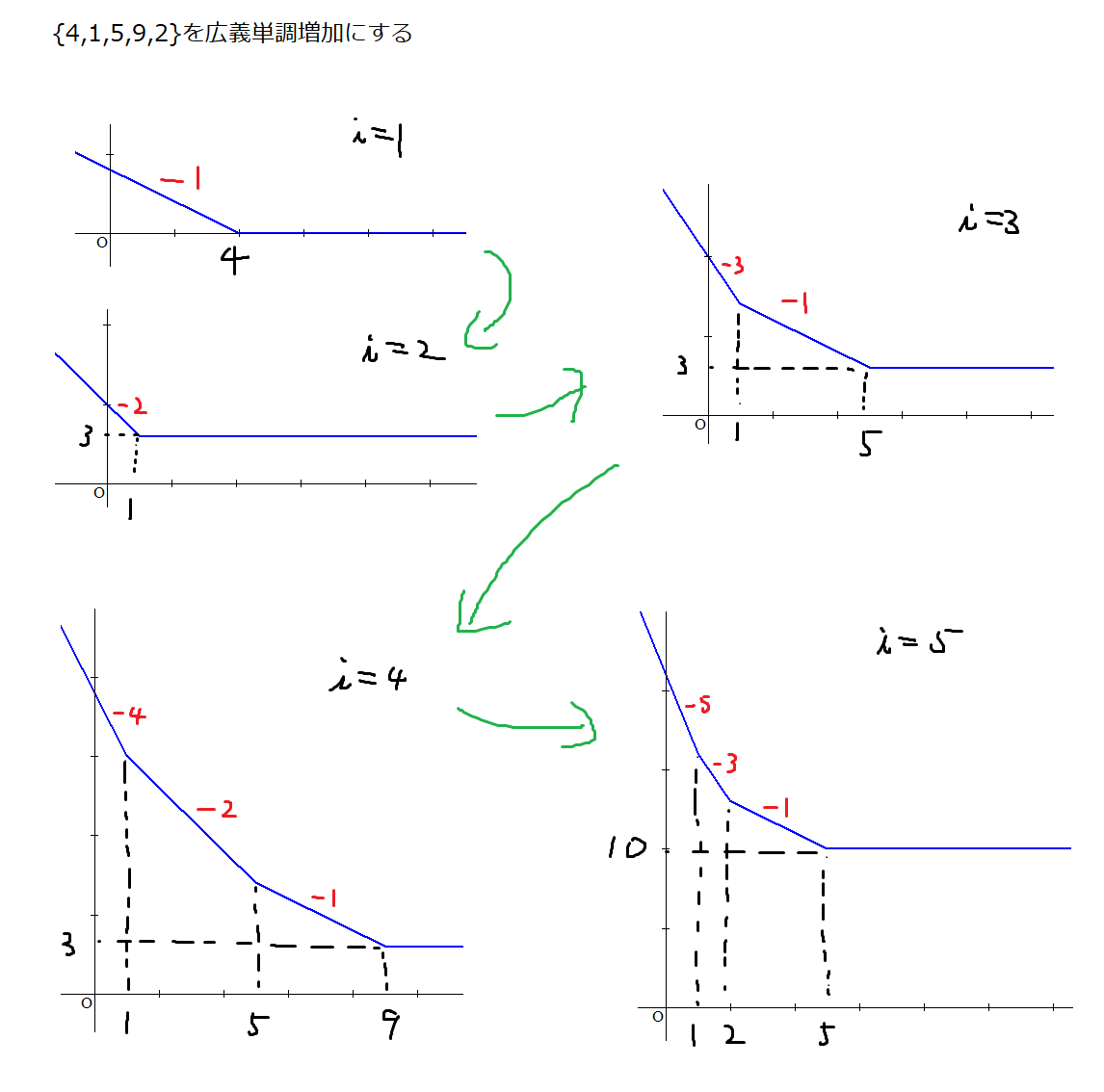
4 1つのオプションは、 diff 関数を使用してベクトル内の隣接する要素間の差異を与えることです。

以下の例から明らかです。

つまり、単調増加関数は狭義単調増加であるとは限りませんし、単調減少関数は狭義単調減少であるとは限りません。

雰囲気でわかると思うが。

最小値のユニーク性は1次変数のときと全く同じ。

先に示したように、この関数は狭義単調増加であるため単射です。

ゆえに半正定値。

先ほど、この関数が単調増加であることを示しましたが、これは狭義単調増加関数でもあります。

狭義単調増加かつ狭義単調減少であるような関数は存在しないため（演習問題にします）、ある関数が狭義単調であることは、その関数が狭義単調増加もしくは狭義単調減少のどちらか一方であることを意味します。

上の証明を真に不等式が成立するとして考えればOK。

狭義単調減少関数が単射であることも同様にして示されます。

微分係数が接線の傾きを表していることを考えれば納得できる事実です。

よって，広義単調増加かつ広義単調減少。

逆は証明を後ろからたどればよい。

unsorted -xx user system elapsed 2. unsorted は明示的に順序を増やしています。

713 厳密に増加するシーケンスを強制したい場合は、 strictlyに? 同値命題 特に狭義凸関数の場合• 単調増加，単調減少に関連する性質 単調減少についても同様なので，単調増加についてのみ述べます。

単調関数と狭義単調関数の関係 狭義単調増加関数は単調増加であり、狭義単調減少関数は単調減少です（演習問題にします）。

unsorted -xx user system elapsed 0. 証明 最小値はただ一つ 最小値が2つ存在するとする, i. 不等式 を考えることができる。

単射の定義域を制限してもそれは相変わらず単射です。

つまり， x x x が増えると y y y は減るような関数です。