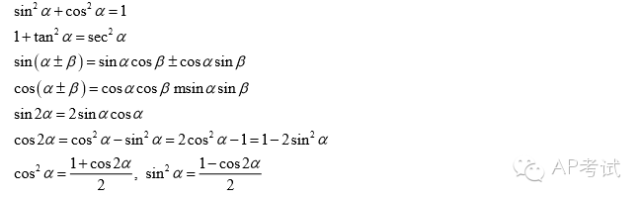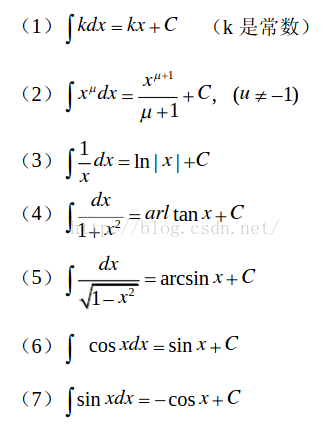微分 積分 公式 - 分かりやすい微分積分

つまりｘ 0＜a＜x＜ｂ に位置付けして考える。

本当は証明すべき事柄ですが，便利なのでガンガン使わせてもらいましょう！ 位置エネルギーと積分 次は仕事について。

先の例でいえば、走行時間と距離の関係（図２）を微分して走行時間と速度の関係（図４）を得たが、逆に走行時間と速度の関係（図４）を積分して走行時間と距離の関係（図２）が得られる。

ただし，感動の勢いあまって「物理の本質は微積分！」などと言い出さないようにしてください笑 物理の本質はどこまで行っても現象の理解。

距離の情報（ある時間にどの位置にいたか）がわかっていれば、特定の瞬間における速度を求められます。

これらをｘ＝aにおけるｆ（Ｘ）の 微分係数と呼ぶ。

そしてこの接戦の勾配こそが、その点における速度を表す。

6 合成関数の規則 初めての方は、下記の一般規則の導出はサラッと読み進めて、積分までの全体像の把握を再優先にして下さい。

このとき、時間が経てばそれに応じて距離が変わるので、時間ｘを 変数と言い、距離ｙはｘの 関数とよぶ。

） 保存力ってなんだっけ？という人は積分してる場合じゃないので，ただちに復習してください！ 交流回路と微分 微分積分の活躍の場はなにも力学だけではありません。

まとめ 積分の範囲の中でも面積ではないのであまり出てこない、しかし忘れた時にやってくる定積分の微分を今回は扱いました。

図３ Ｐ点での速度の求め方 図３は図２と同じ走行時間と距離の関係のグラフであるが、中間点である０．５時間での速度の求め方を図示している。

Contents• ハイ，運動量と力積の関係が出てきましたよっと。

あれ、不思議ですね。

他の時間でも時間と速度の積であるから、それで形成される長方形の面積を求めればよいことが分かる。

微分方程式を学ぶときに必須となるので、必ず覚えておいて下さい。

変更する場合があります。

商の微分公式の覚え方 ・1について これは頑張って覚えて下さい。

・微分・積分の公式を一緒に覚えられるように，教科書でよく見るような公式の形とは変えています（もちろん意味は同じです）。

したがって数学や科学の専門でない一般の人でも、 微分・積分とは、およそどんなことで、何故必要なのかを知ることは大事だと思う。

微分法の一般規則と導出 微分公式と同様に、式 1 の導関数の定義式から、下記の一般規則を導くことができます。

それはこれから順次説明していくが 微分とは数学的な手段であり計算によってその変化率を求めることができるからである。

記事の最初に確認したイメージを、ニュートンは考えていたわけですね。

次の例も同様です。