扇形 中心 角 求め 方 - 【カンタン公式】扇形の中心角の求め方がわかる3つのステップ
中学1年生数学
また、「弧」は円周の一部であることもわかるでしょう。
そして大きさの比が面積や弧の長さの比になっているのです。
26㎠です。
ものすごく簡単で便利でしょ?? 公式をつかわない!扇形の中心角の求め方3つのステップ それじゃあ、なぜこの公式で扇形の中心角が求められるのか?? ちょっと気になるよね?? じつは、扇形の中心角の公式は、 比例式をつかった中心角の求め方 から導きだしたものなんだ。
扇形の中心角の求め方の公式ってなんですか?
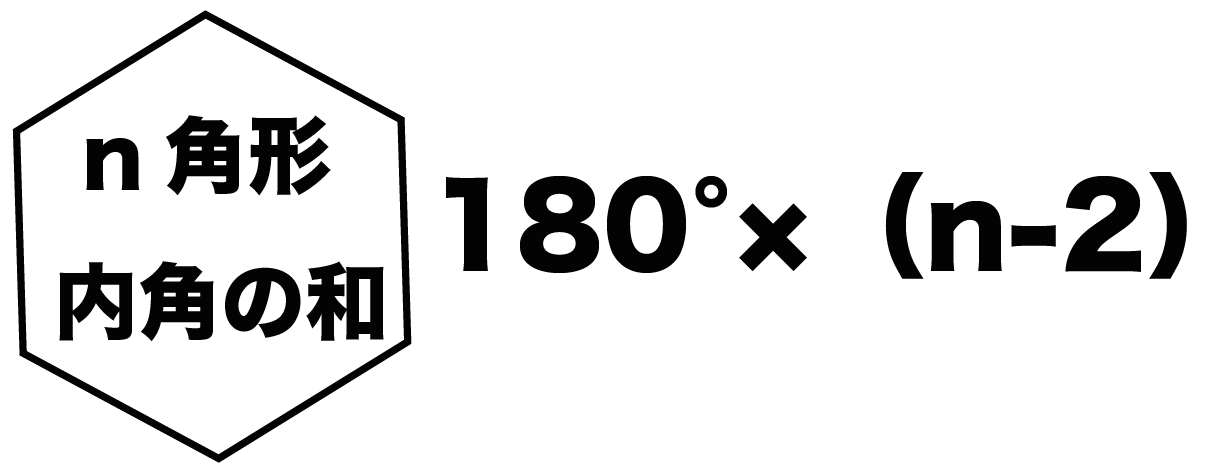
ぐるりと丸い円を描くと、円の大きさにかかわらず、その中心角は360度です。
「なんでこの公式で円の面積が求まるんだろう?」と感じる方も多いのではないでしょうか。
扇形の平面図形もまた、ひっかかりやすい問題のひとつです。
とりわけ、円周率が出てくると計算が煩雑になるため途端にミスが増えるのです。
おうぎ形の弧の長さ、面積、中心角の求め方と公式
42㎠です。
あとは、 xを求める方程式を解いていけば良いです。
練習問題で理解を深める! 面積が与えられているので円の面積と比較していきます。
半径が4cmで弧が18. それでは、中心角、孤長のどちらかを上記の式を用いずに求める方法はあるのでしょうか。
【おうぎ形】中心角を求める3つのパターンを解説!方程式で解く?比を使う?
「扇形の弧の長さ」は「中心角の大きさ」に比例する、 っていう性質をつかってあげよう。
円周と弧の長さの比は中心角が基準となっているということを抑えておきましょう。
なぜなら、円錐の問題には 空間図形の知識だけでなく、おうぎ形の知識も一緒に問うことができるからです。
今回は、みんな大嫌いおうぎ形についての解説です! なんで、おうぎ形って苦手な人が多いのでしょうかね? やっぱり公式を覚えたりするのが難しく感じるのかな? そんなおうぎ形の問題の中でも ほんと正解率の低い『中心角を求める』という問題にスポットを当ててみたいと思う。
扇形 半径 求め方 930452
おうぎ形の練習問題 問題1 4cmだった。
中学校の扇形の中心角と半径の出し方についてです。
どうやって解けばいいかわかりやすく 教えて下さい。
弧の長さが与えられている問題では、弧の長さと円周の長さで比を取るようにしてください。
おうぎ形の弧の長さ、面積、中心角の求め方と公式
底面の円周の長さを求めて、側面の弧の長さを求める• 扇形の面積を求める公式に代入して、計算すればいいだけですね。
方程式を利用し求めるパターン• 問題 下の図の立体についてそれぞれ求めなさい。
どうですか? 今までのパターンに比べたら格段に簡単になったと思いませんか? そう思えた方は今後、このパターンを使いこなしていってください。
中心角を求めよう! 弧の長さの公式を用いた解き方 それでは実際に中心角をどのように求めたらよいのかを見ていきましょう。
- 関連記事
2021 tmh.io