区間 推定 - 母平均の区間推定 統計学入門

１．母比率の区間推定 例 ある薬で１００人のうち４０人が副作用がみられた場合の、副作用発生率（p）を９５％信頼区間で示す。

そこで次回は、サンプル調査から得た「標本平均」をより信頼性のある指標にするための対応策を紹介していこう。

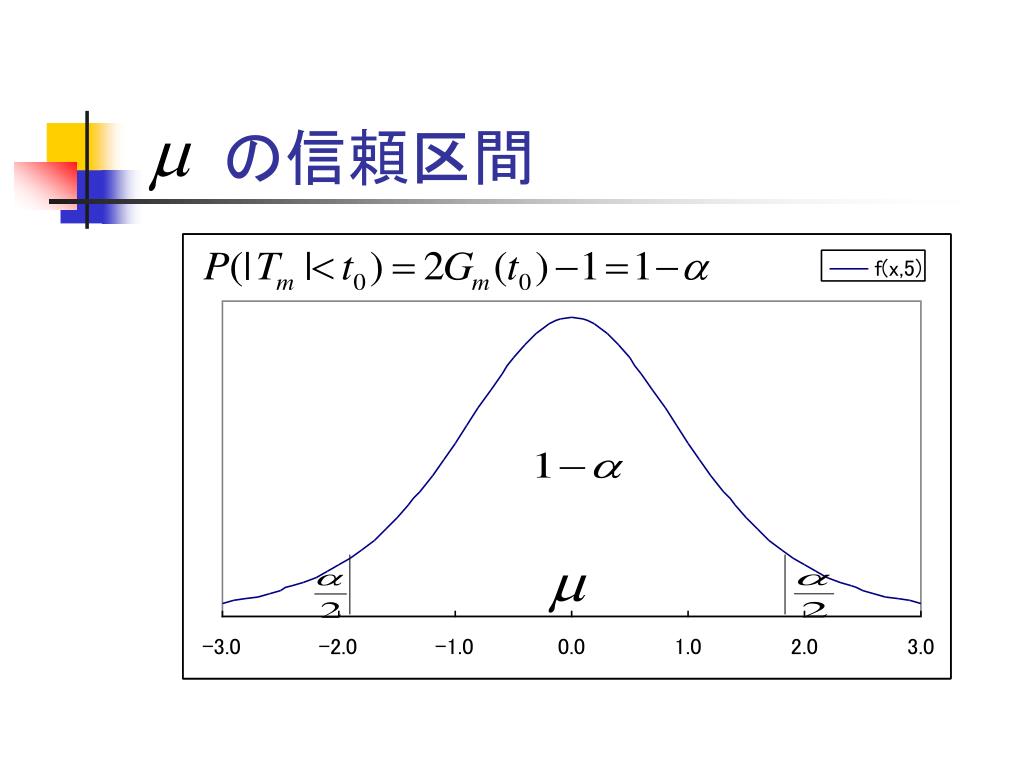
自由度と検証したい確率がクロスするところのt値を読み取る。

54までの間に含まれるということです。

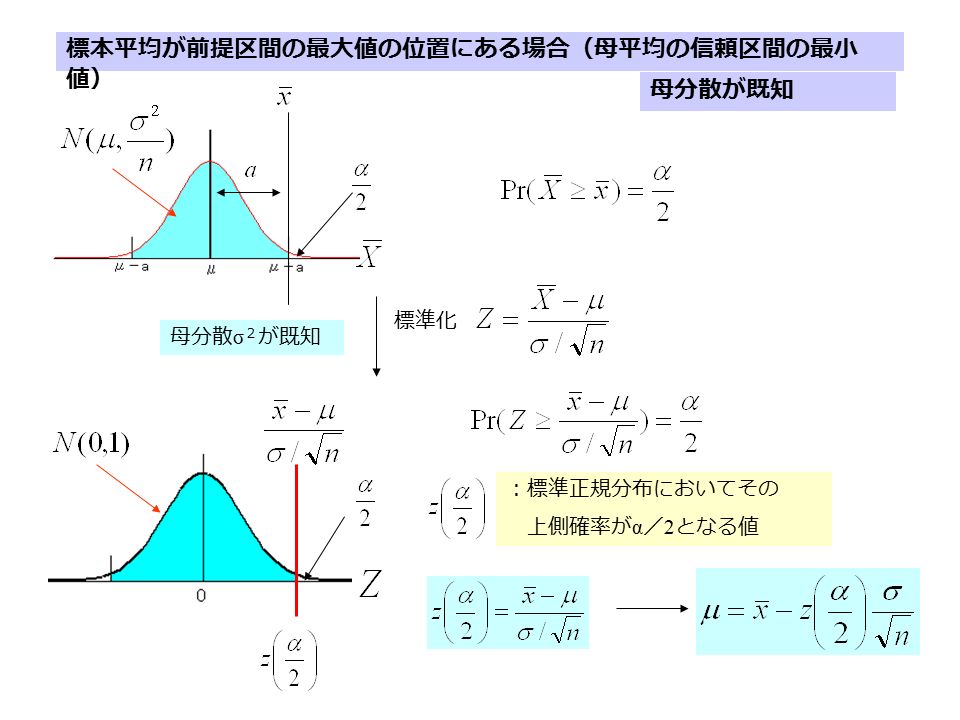
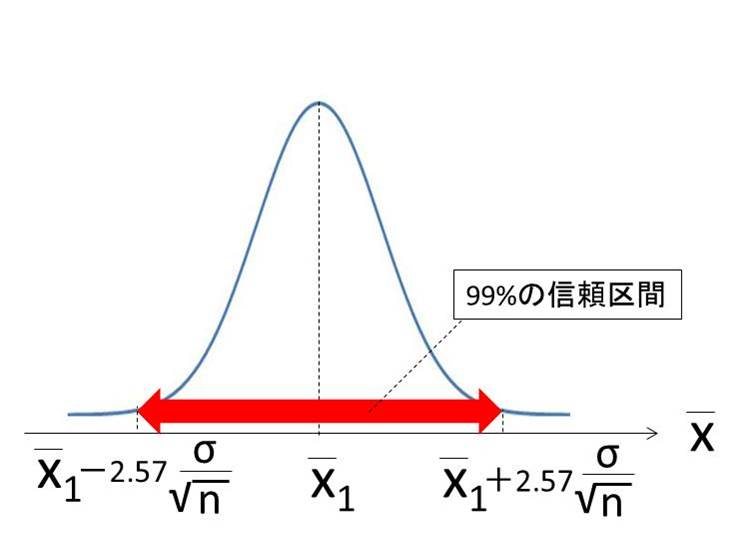
「信頼区間の最大値」の算出• ただし、ここで話していることは「信頼区間の意味」というイメージづくりをしているにすぎないので、厳密にいうと、計算が異なります。

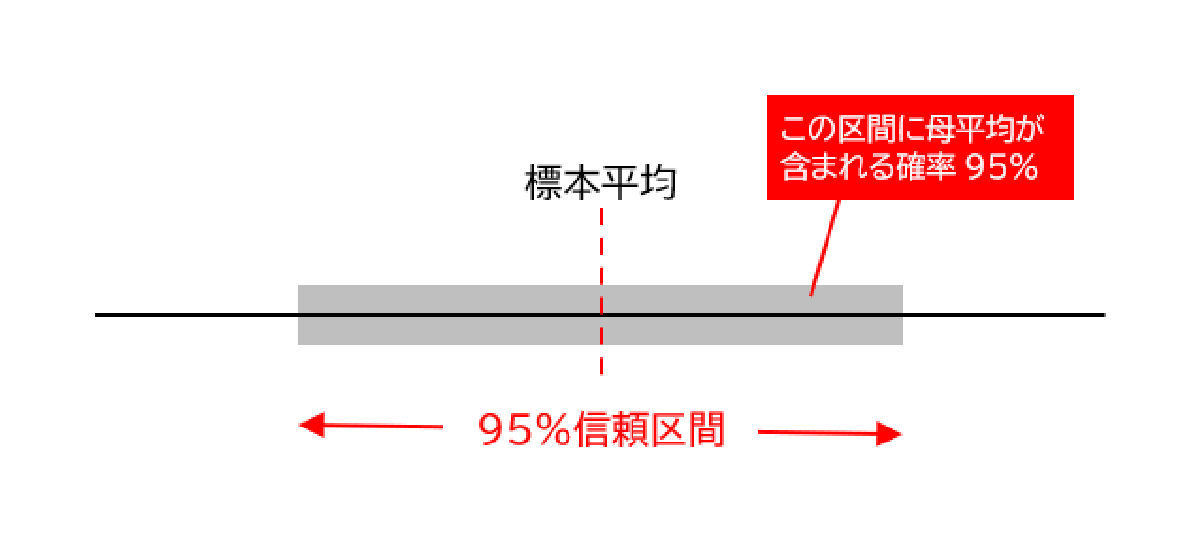
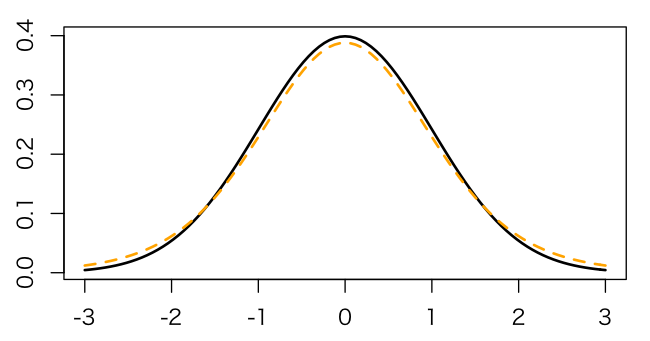
たとえば、標本平均が下の図のように母平均から少しずれていたとしたら矢印の範囲を指定すれば、母平均を含んでいることになります。

そのときの平均値は母平均に一致します。

平均値の誤差の算出 あとは、この数値を「標本平均」にプラスマイナスするだけだ。

僕ら個人が行う調査は、「」の考えに基づいて行われます。

いま、標本平均をひとつ取ったとすると、その値は下の標本平均の分布図の矢印の範囲内に大体はいります。

05をみて、これらがクロスする部分に記載されている数字がt値となる。

このようなことを何回も繰り返します。

ここまで、標本を何回も取ることを考えてきましたが、通常私たちが標本を取るのは一回限りのことです。

標本平均の分散 標本平均の標準偏差 標本平均の標準偏差を標準誤差（SE:Standard Error）という。

次に、サンプルサイズを10として、母集団から10個のデータを取ります。

少し回りくどい表現であるが、要は「標本平均にある程度の幅をもたせてあげる」という考え方だ。

Excel 実験データを解析時に確認する15個の指標 先ずを計算しました． 中央値と算術平均値がほとんど同じで， 尖度・歪度ともに-1. 推定とは、確からしい値を標本から導く方法で、点推定と区間推定がある。

前回の連載でも紹介したように、「不偏分散」は関数VAR. そこで、5％くらいは妥協して推測を進めていくのが「95％信頼区間」となる。

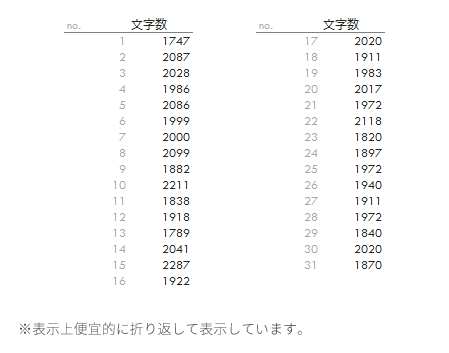
以下のような表だ。

逆にサンプルサイズが大きいときは正規分布に近づいていきます。

信頼区間ってどういう意味があるのか？ この疑問を解消することができます。

今回の例における「平均値の95％信頼区間」は68. 信頼区間って何？• よって、関数SQRT を使って以下のように数式を入力すると、「標準誤差」を求めることができる。

」 「いいかえれば、20回に1回はハズレになるわけですが、それでよしとするということです。

ある標本より母集団の平均や分散を推定することができる． 平均値の最もありそうな値を決めるのが点推定であり、 平均がある確率で存在する範囲を決めるのが区間推定である．９５％で存在する場合９５％信頼区間というが９０％信頼区間も利用される．信頼区間の上限と下限を信頼限界という． 区間推定や信頼区間を理解するには、少なくともを理解しておくことが重要と思われる。