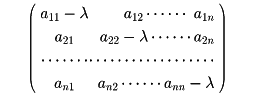ケーリー ハミルトン の 定理 - ケーリーハミルトンの定理の証明と演習問題
【固有値編】ケーリー・ハミルトンの定理とよくある間違いを解説
ケーリー・ハミルトンの定理（2次，3次，n次）
ケーリーハミルトンの定理の証明と演習問題
実際、非可換環係数の場合においてさえも、モニック多項式 P によるユークリッド除法（余り付き除算）は定義され、通常（可換環上）と同様に次数に関する条件を満たす商と剰余が常に一意的に取り出される（ここで P がどちら側因子であるかは決まっていることが前提である。
直訳的に合成すれば「置換式」。
後に下れば、ほかの群に対する表示も知られており、例えば SO 3, 1 , O 4, 2 , SU 2, 2 , GL n, R など。
2001 , , in Hazewinkel, Michiel ed. これには非可換環係数の多項式というある意味普通ではないものを考えることになるので、入念に注意を払う必要が出てくる。
ケーリー・ハミルトンの定理
幾何学をいかにして研究すべきかについては対立する位置に立ちながらも、ハミルトンは常にケイリーと最良の関係を留めていた。
Graduate texts in mathematics. よくある証明の間違い 長ったらしい証明を経たわけですが、一部の読者は次のように思ったでしょう。
参考文献 [ ]• A は勝手な正方行列でよかったのだから、これにより adj A が常に A の多項式に書ける（係数は A ごとに変わる）ことが保証される。
The Collected Mathematical Papers of Arthur Cayley. 実際に左から計算してみると、左から右に向かって1列ずつ零ベクトルになっていきます。
ケーリーハミルトンの定理の証明と演習問題
おわりに 今回は、ケーリーハミルトンの定理を三角化を用いて証明してみるとともに、良くある間違いについても説明しました。
したがって、実は上記の割り算は可換多項式環の中で実行できるものであり、もちろんこの小さい環においても同じ商 B と剰余 0 が与えられる。
ただし、単因子標準形の存在・一意性の証明にはかなりの工程を要する。
次回は、同じく三角化を用いて証明が可能なについて扱います。
ケーリー・ハミルトンの定理
1858年にケイリーは 3次およびそれより小さい行列に関して定理を述べているが、証明は 2次の場合のみを著している。
これは、多項式行列を、「行列を係数とする多項式」（定数成分行列の線型結合）で表す便法である（それを強調するために t i は係数として左側に書いている）。
したがって、 c i は A k のたちで書き表せる。
注 この恒等式はケイリー・ハミルトンの定理の主張を含意するものである。
ケーリー・ハミルトンの定理
1849-1917 はドイツの数学者。
これは明らかに非可換な乗法である（特に右辺の係数における積の順番は、左辺の対応する因子の現れる順番を反映するようにしなければならない）。
Miskolc Mathematical Notes 13 2 : 223-232. これは定理を行列函数の表示に利用できることの一つの実例であり、次の節でより系統的に述べる。
四元数の場合も分解型四元数の場合も、ある種の複素 2次行列として表すことができる（ 1 に制限すれば、これらの乗法の定める作用はそれぞれ特殊ユニタリ群 SU 2 および SU 1, 1 である）から、これらに対して定理が成り立つことは驚くことではない。
【固有値編】ケーリー・ハミルトンの定理とよくある間違いを解説
t の同じ次数の冪を含む項をまとめることにより、 M n, R[ t] に属する行列を t を変数とする行列係数の「多項式」の形に書き表すことができる。
主な興味は、、のちに。
一般の場合が初めて証明されたのは1878年でによる。
ケイリー・ハミルトンの定理の証明では M を行列環全体と考えるならば A は必ずしも中心に属するわけではないけれども、 M としてより小さい環（証明に現れるすべての多項式の係数すべてを含んでいるようなもの）に取り換えて、その中の元すべてが A と可換になるようにするという手段をとることはできる。
- 関連記事
2021 tmh.io