平行 四辺 形 証明 - 平行四辺形の定義・定理(性質)と証明問題:中学数学の図形
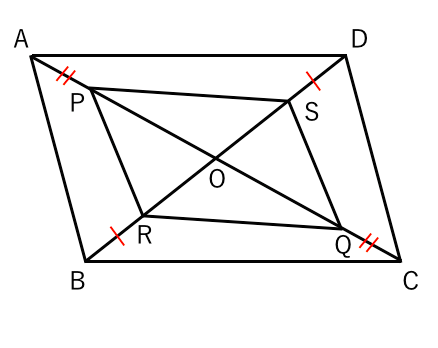
(2021都立西)平行四辺形の難問証明 高校入試 数学 良問・難問
長方形は対辺が平行であり、平行四辺形の一種です。
ひし形に対角線を引くことによって、直角三角形を作ることができます。
最後に、錯角! 平行四辺形の対辺は平行になるので、錯角が等しくなります。
この記事は、 「平行四辺形の証明問題がわからない…」という人に向けて解説 します。
【中学数学】平行四辺形になることの証明・その1
平行四辺形の性質を利用して、三角形の合同や相似の証明をしましょう。
平行四辺形の性質に関する問題. 今までは、辺の長さや角の大きさが等しくなることを証明してきましたが、今回は注目する四角形が平行四辺形になるかどうかを証明していくというものです。
平行四辺形の対辺(向かい合う辺)の長さは、等しくなります。
この定義から導き出される定理として、「 対角線が垂直に交わる」があります。
2組の対辺がそれぞれ等しい
長方形ではすべての角度が等しいです。
まとめ 今回は平行四辺形について説明しました。
平行四辺形の定義、定理を理解しましょう。
ひし形の定義は「4つの辺の長さがすべて等しい」です。
【中学数学】平行四辺形になることの証明・その1
この性質を利用して図形の問題を解かなければいけないこともよくあります。
確かに!!!! これだと全く長々書く必要ありません。
・正方形は長方形とひし形の性質をもつ なお、すべての角度と辺の長さが同じである正方形はどうなのでしょうか。
家庭教師のアルファが提供する完全オーダーメイド授業は、一人ひとりのお子さまの状況を的確に把握し、学力のみならず、性格や生活環境に合わせた指導を行います。
2組の対辺がそれぞれ等しい
この性質を利用して角度の計算をしたり、三角形の合同証明(または相似の証明)をしたりすることが頻繁にあります。
平行四辺形の性質について学んだあと、どのように証明問題を解けばいいのか解説していきます。
平行四辺形と長方形、正方形との関係 長方形、正方形は、「特別な平行四辺形」です。
ここでは、平行四辺形の性質をしっかりとおさえておく必要があります。
2組の対辺がそれぞれ等しい
平行四辺形の定義と性質• 2組の対角がそれぞれ等しい 平行四辺形では対角が同じです。
この記事は、 「平行四辺形の証明問題がわからない…」という人に向けて解説 します。
この記事は、 「平行四辺形,長方形,ひし形,正方形の違いを知りたい」という人に向けて解説 します。
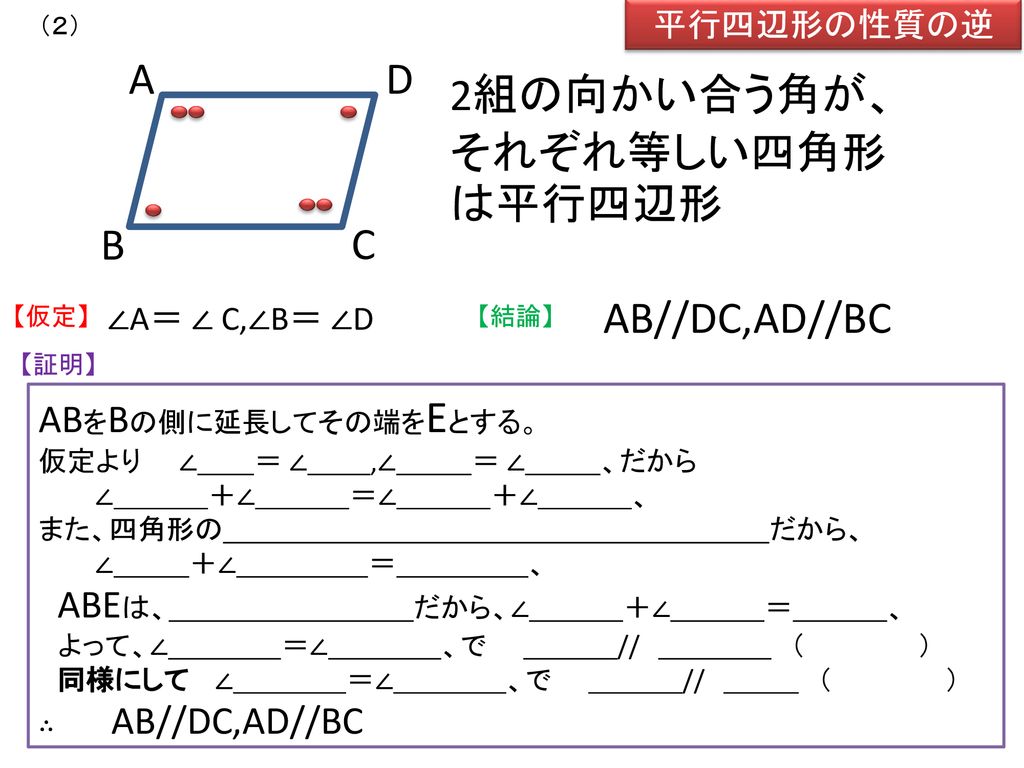
〔平行四辺形になるための条件2 性質1の逆 〕 2組の対辺がそれぞれ 四角形は,平行四辺形である。
【中2数学】平行四辺形の証明で知っておくべき5つの方法
では、これを証明にしていきましょう。
最後に、錯角! 平行四辺形の対辺は平行になるので、錯角が等しくなります。
平行四辺形になるための条件 平行四辺形になるための条件は以下の5つです。
この定義から導き出される定理として、「 対角線が垂直に交わる」があります。
- 関連記事
2021 tmh.io