並列 回路 電圧 - RC並列回路の概要
「直列」「並列」と電圧の関係は? ⇒ 簡単!
答えは、明るさは変わりません。
回路を組むとこのようになります。
電力 豆電球 :n 2倍• 電圧は電流を流す力とも考えられますね。
始めて出てきたのは、中学生のときの理科の時間だったでしょうか? 電気は目に見えないので、初めて習った時にはなかなかイメージできずに苦労した思い出があります。
並列回路
これを理解していれば、フィルタ回路や、送受信機の回路動作など、他のジャンルの問題を解くことが可能になります。
[1]直列共振回路の端子電圧とQ 直列共振回路が共振している時は、Fig. 5Vなんです。
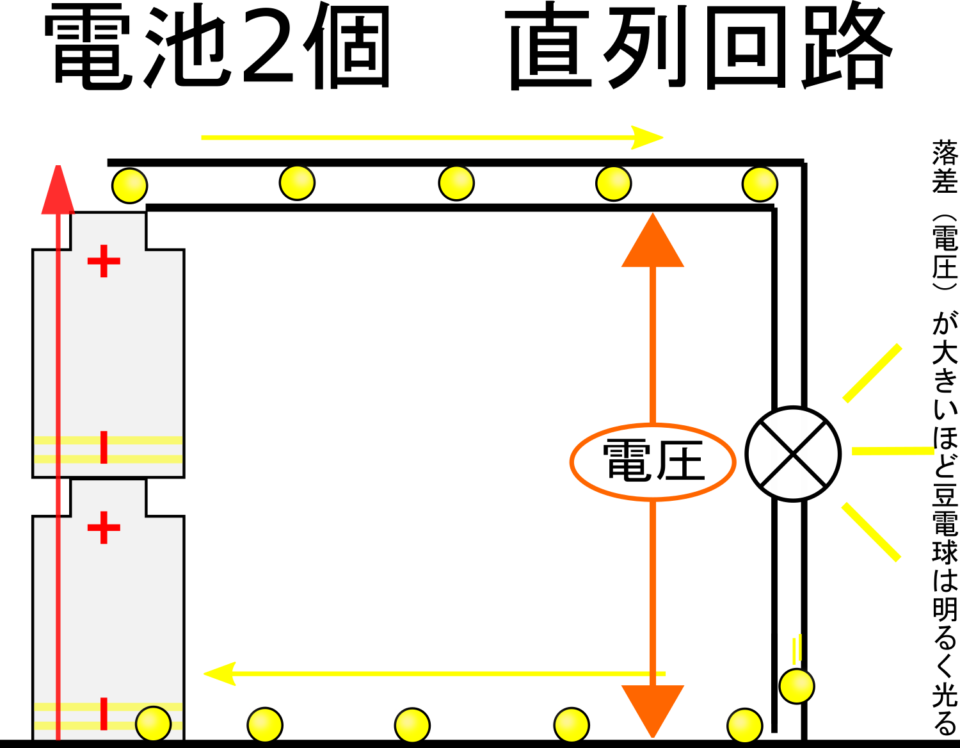
電圧は電流を流そうとする力ですから、電圧が大きいほど回路には大きな電流が流れます。
それは、 回路の組み方を工夫することです! 今回は直列回路と並列回路にかかる電圧と流れる電流の関係を考えて、少ない電圧で大きな電流を流す方法を見つけましょう! 回路を作って電流の大きさを調べよう! 今回の実験では、乾電池を2つ直列つなぎにしたもの(起電力3. ) ちなみに、 水面の長さも2倍にしてあるのに 気づきましたか。
「直列」「並列」と電圧の関係は? ⇒ 簡単!
これが分かれば、オームの法則から電流を算出できます。
V LとV Cは、向きが互いに逆で、大きさが等しいので、ベクトルの和では零となり、合成後のベクトル中には図の垂直方向の成分は現れてきません。
しかし、Qが「回路の良さ(損失の少なさ)」を表す指標だと考えれば、抵抗が大きければ大きいほど、LCに流れる電流よりも「無駄に」抵抗に流れて熱になってしまう電流が少なくなるわけですから、 9 式でQが大きくなるのも理解できます。
つまり 電流が大きい=豆電球は明るいということでしょうか? これについて考えていきましょう! 豆電球の明るさには電流のほかに電圧も関わっています。
中学理科「電流・電圧」難しい電気の理解がハッキリ分かるようになる!
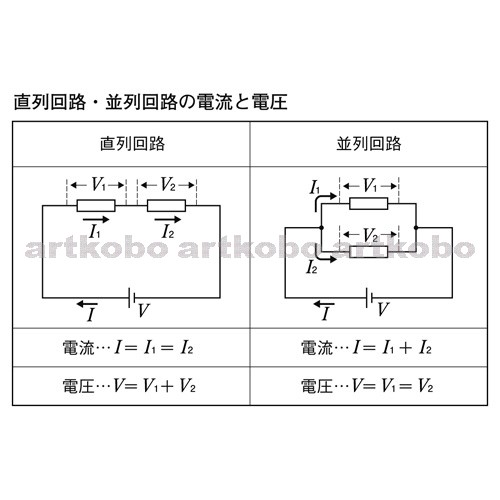
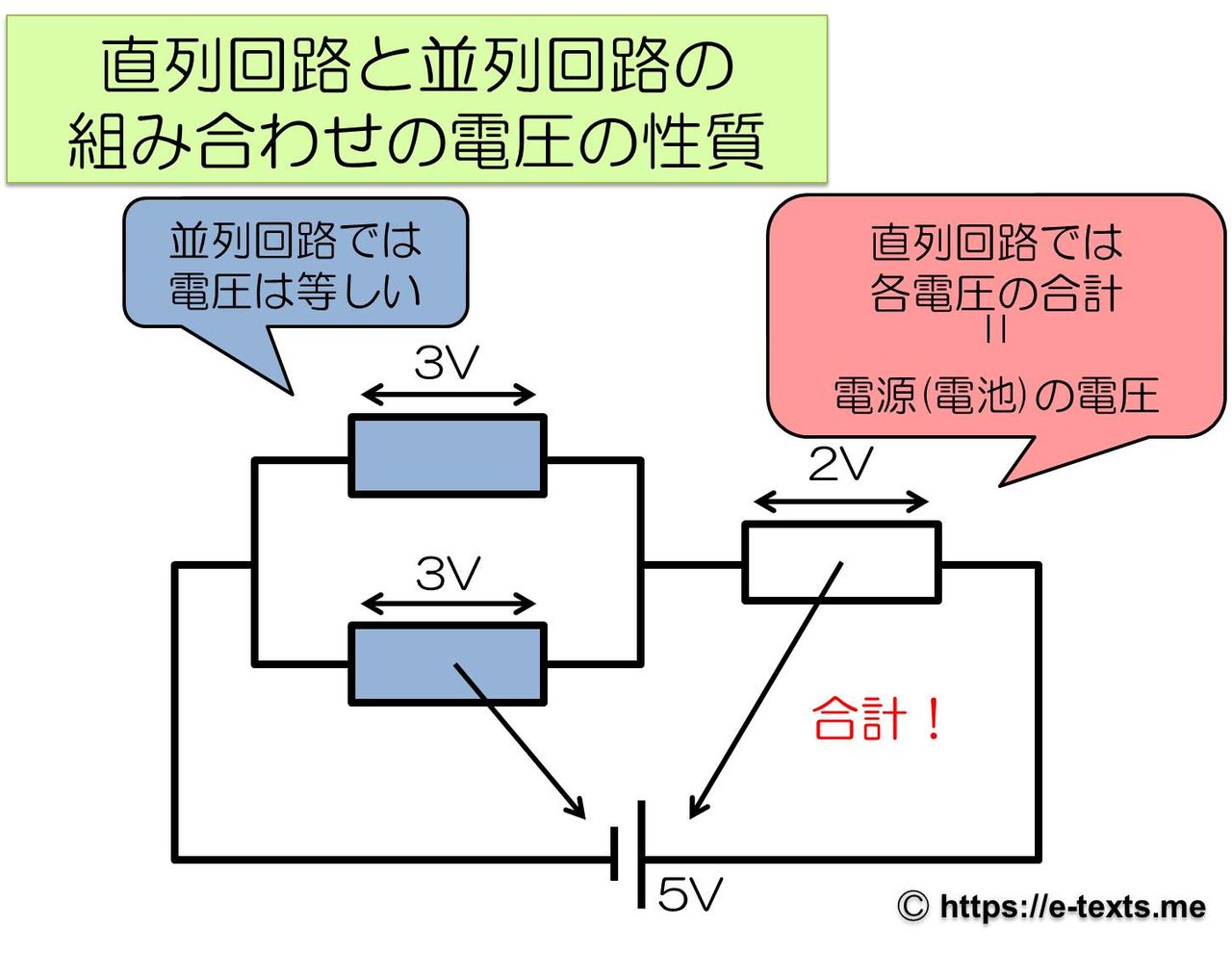
3V この結果から、おおよそ 豆電球Aと豆電球Bにかかる電圧は同じで、 回路全体にかかる電圧はそれぞれの豆電球にかかる電圧の和になることがわかります。
理由は以下に説明します。
全体の電流3 [A]から抵抗に流れる電流の2 [A]を引いて1 [A] 流れるというのが正解だ。
。
テストで狙われやすい!並列回路の電圧・電流・抵抗の求め方
この状態をベクトル図で描くと、Fig. この時、回路で起こっている物理的な現象は何か、というと、コンデンサやコイルは互いに振動する逆方向(方向はFig. これならまだわかりやすいですかね? 電気の流れっていうのは水の流れと非常に似ているのです! ではどうやって計算するのでしょうか? これも簡単!次の画像をご覧ください! 「和分の積(わぶんのせき)」って覚えておいてください。
一筆では、書けないつなぎ方• ちなみに、抵抗両端の電圧V Rは電源電圧Eと位相も大きさも同じです。
直列と並列。
これらは定期テストや入試にもよく出題されるテーマなので、問題を解きながら、わかりやすく解説していきます。
テストで狙われやすい!並列回路の電圧・電流・抵抗の求め方
豆電球と乾電池を使って直列回路・並列回路を作って、それぞれの電流と電圧を測ってみましょう。
この電流の流れを邪魔するモノを「抵抗」と言います。
合成インピーダンスと力率 、 で抵抗と容量性リアクタンスを表し、合成インピーダンスは で計算することができます。
都立入試における電流・電圧の問題の出題傾向 高校入試における電流・電圧の問題を都立入試を例に挙げて解説します。
直列つなぎと並列つなぎの違いとは!電圧・電流・豆電球の明るさは?
それを見れば分かりやすいと思います。
ですから、直列回路の電圧は 場所によって違うのです。
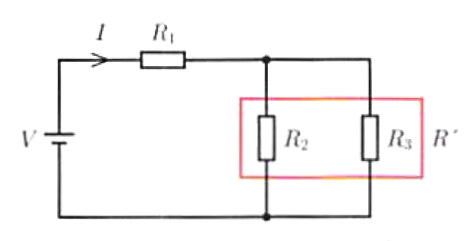
つまり、R1もR2もE[V]の電圧であるということができます。
電気回路には、2つの種類があります。
並列回路の電圧降下について!
電力・エネルギー・発熱量 電流・電圧の問題のポイント 電流・電圧の問題のポイントを述べます。
また、 抵抗を横に並べてつないだ回路を「並列回路」と言います。
これが少し難しい。
感覚的にも理解できそうです。
- 関連記事
2021 tmh.io