平行 四辺 形 公式 - 平行四辺形の面積の公式|なぜ『底辺×高さ』で求められるのか?|数学FUN
平行四辺形の面積の計算|もう一度やり直しの算数・数学
が大きいです。
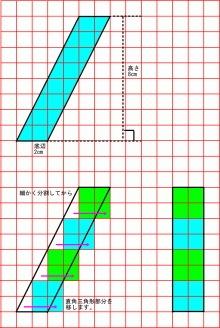
下の図のように、2つの直角三角形と長方形に分けてみます。
そして、この図を見て、 正方形が置けるように赤い三角形を動かせないか? を考えてみてください。
証明は対角線によって、平行四辺形を2つの三角形に分け、その三角形の合同を示すことでできます。
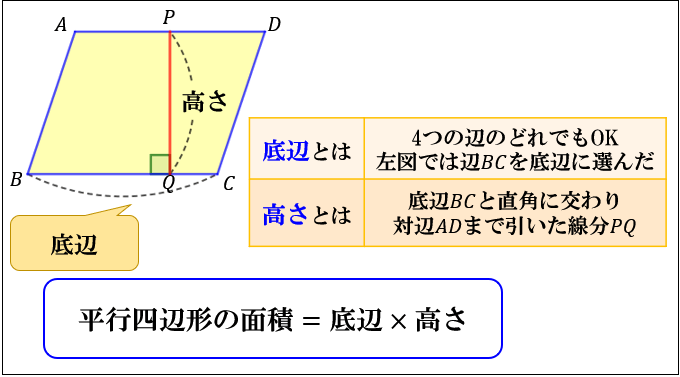
平行四辺形の面積の公式
」 見えましたか? この問題では、2種類の辺の長さが与えられていますが、面積を求めるには、対応する高さが存在する辺を選ぶ必要があります。
平行四辺形の法則とは、2つの力(2力)を2辺とする平行四辺形の対角線が「2つの力の合力になる」法則です。
1点に2つの力が作用しています。
言葉だけで覚えるのは難しいと思うので、図とともに理解しながら覚えておきましょう。
平行四辺形の面積の求め方【公式】
…と、説明したものの、下のような平行四辺形だと、先ほどのように三角形をいい感じに切り取ることができませんね。
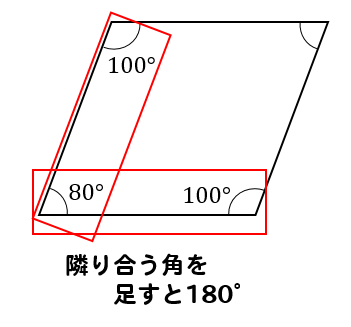
平行四辺形の成立条件その3:2組の対角がそれぞれ等しい 今回の条件は 「2組の対角がそれぞれ等しい」ということで、これを使います。
冒頭の公式 1 1 1 2 2 2 の証明には,この公式を使います。
上図のように底辺と斜辺のなす角度は30度です。
平行四辺形の面積の公式はイメージでとらえること
成立条件は全部で5つあります。
【説明1】台形2つで平行四辺形になる 台形と合同の図形を180度ひっくり返してくっつけたら平行四辺形になります。
下の図のように、平行四辺形の一部を三角形に切り取って、移動させてみましょう。
逆に、平行四辺形の法則を用いて1つの力を2力に分解することも可能です。
平行四辺形の面積の求め方
さて、平行四辺形の面積の公式は何ですか?ちょっと大人の方でも忘れてしまって思い出せないという方もいるのではないでしょうか!?たしかに面積の公式ともなってきますと、パッとは思い出せないかもしれませんが、図形のイメージを思い浮かべてみると意外と記憶に残りやすいと思います。
しかし, 三点を同じ方向同じ距離だけ平行移動しても三角形の面積は変わりません。
四辺形(4つの辺から成り立っている多角形)である• 平行四辺形の成立条件その2:2組の対辺がそれぞれ等しい かなり簡単に証明をします。
また、対称の中心 回転の軸 は、 対角線の交点 中点 に等しいということも特徴の1つです。
【3分で分かる!】平行四辺形とは?定義や性質・成立条件をわかりやすく
丸暗記していたらいざ本番で忘れた時に解けなくなるので、毎回頭の中で図形の変形をイメージしながら解くのをオススメします。
後の4つの証明は 四角形が平行四辺形の定義を満たすことがゴールになります。
下の図のようになればOKです。
2つの力をP1、P2とするとき、2力の合力は下式で計算します。
- 関連記事
2021 tmh.io