フック の 法則 - 実験13 フックの法則/1年理科『物理学』/takaの授業記録2012
フックの法則|ばねの総合メーカー|フセハツ工業株式会社
タンジェントこのあいまいさのため、上記の2つ数の商の最終的な計算を行う前に、分子 N と分母 D のサインを決定する必要があります。
すると、 K x= k 1+ k 2 xから、合成ばね定数 K= k 1+ k 2のばねがおもりを引くことになるわけですね。
フックの法則は、限定された荷重条件下における幾つかの材料に関してのみ成り立つ。
弾性ポテンシャルエネルギー方程式 他のデータを使用して kを計算することを学習したい場合、弾性ポテンシャルエネルギーの概念は、記事の前半でバネ定数と一緒に紹介されています。
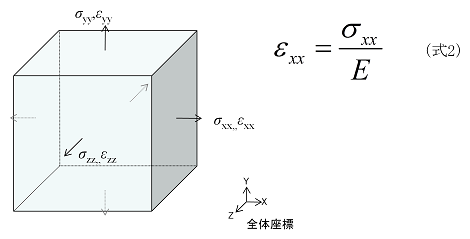
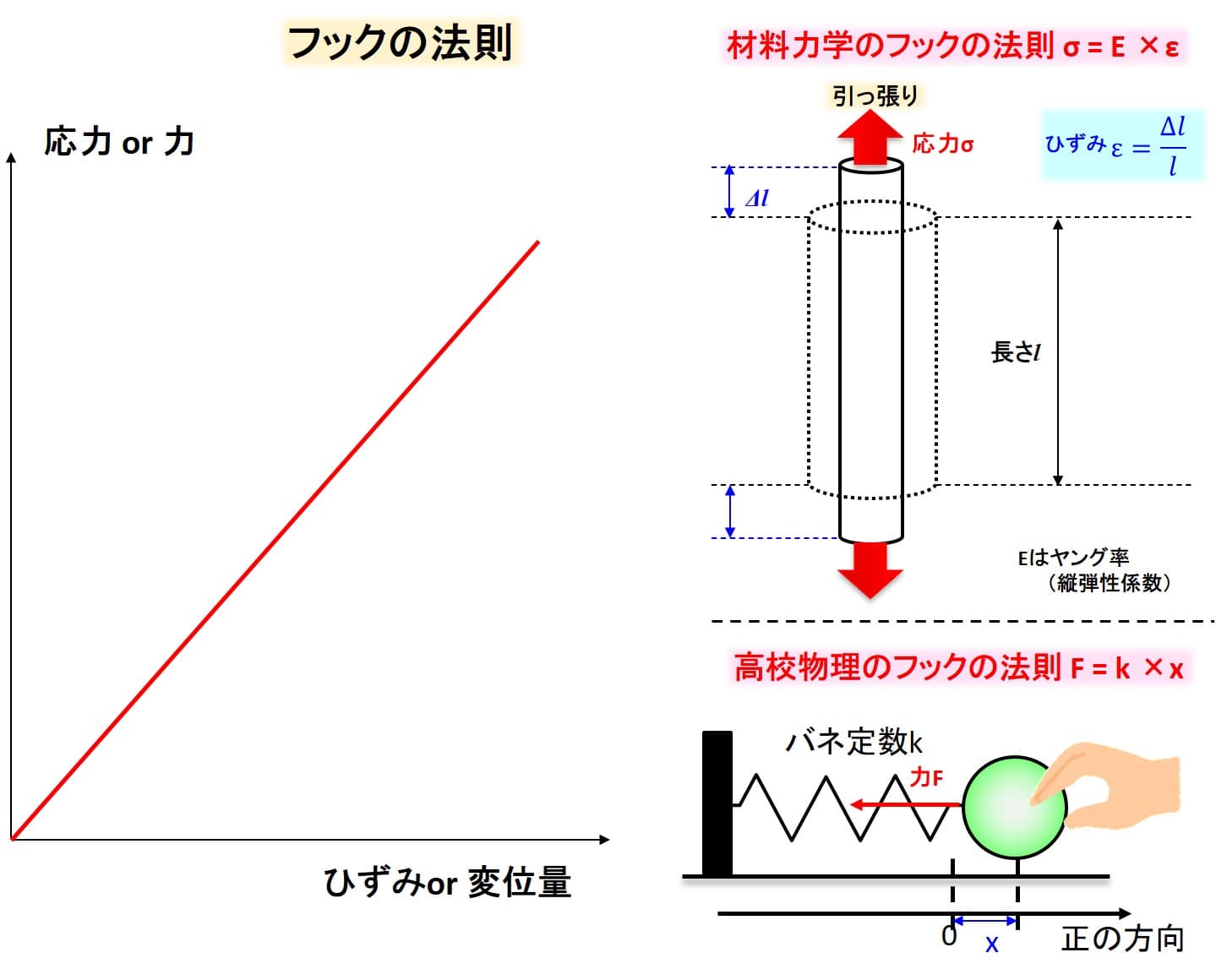
応力とひずみの関係(フックの法則とヤング率)~プラスチック製品の強度設計~
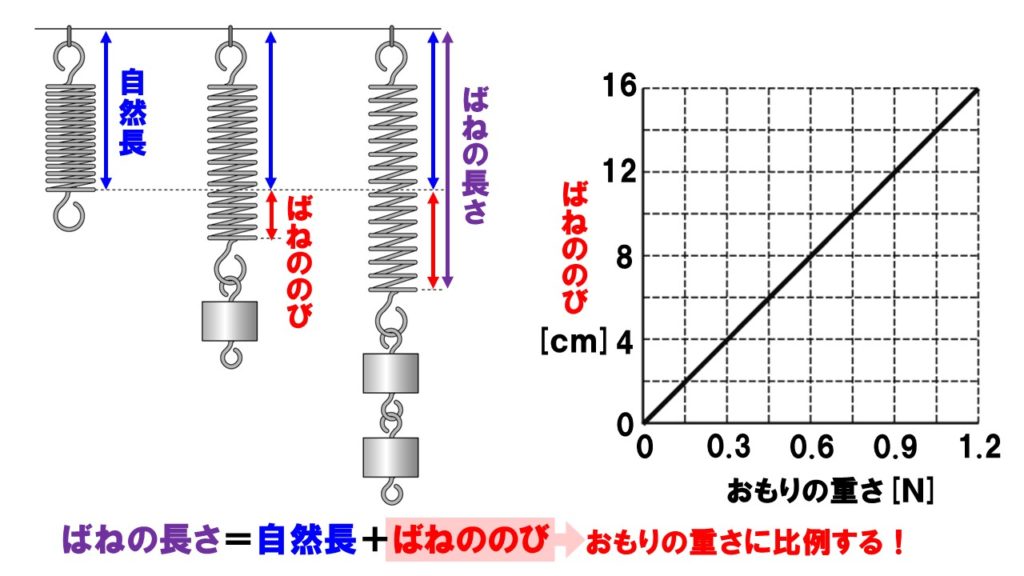
なので、それぞれ2cmずつ伸びるわけです。
この直感的な理解-適用された力が取り除かれた後、弾性材料がその平衡位置に戻るということ-は、 フックの法則によってはるかに正確に定量化されます。
また、反力は常に x変位の反対方向へと働くため、数式の右辺には負の符号がつく(例えばばねを右へと伸ばしたとき、ばねは左に向かって引きつける)。
2人対1人で綱引きをすれば2人の方が勝ちます。
弾性力とフックの法則!ばね定数の求め方と単位!
天井がばねの上端を引く力の大きさは F 2で、ばねの上端が天井を引く力の大きさは F 3ですね。
ひずみ計測による材料応力の決定 ひずみ計測値から材料応力を計算する方法は、材料の弾性変形範囲内では、フックの法則に基づいて行います。
ばねが xの正方向に伸ばされるに伴い、ポテンシャルエネルギーは増加する(ばねを縮めた場合にも同じことが起こる)。
地震の衝撃を和らげる 建築物など• 6 Nの重みはニュートン単位の数値であるため、すぐにそれが力であることがわかり、バネが平衡位置から伸びる距離が変位 xになります。
フックの法則とは?1分でわかる意味、公式、単位、応力、ヤング率の関係
フックの法則の方向 あなたは間違いなくフックの法則のマイナス記号に気づいたでしょう。
彼はニュートンとしばしば研究業績に関して論争をしています。
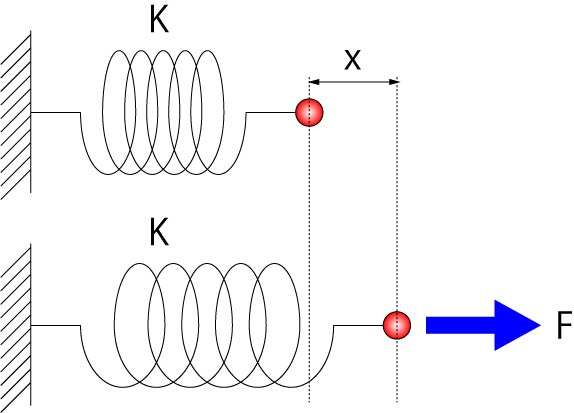
(左図のような装置では実際に引っ張った際には硬いばねの方にワイヤーが片寄ってしまいますが、ここでは理論上、片寄らないで両方とも同じ長さだけ伸ばされることとします。
「力」と「重さ」は、全く同じ概念であることを忘れずに。
フックの法則ってなに?わかりやすく解説
このばねの伸びは x 1+ x 2 ですよ。
科学者は、普遍的な法則を見つけ出す必要があります。
5Nで十分です。
ただ、メインはニュートンとフックの関係性を描いています。
弾性力とフックの法則!ばね定数の求め方と単位!
上記では引張荷重を例に説明しましたが、弾性体ではせん断荷重でも同様にフックの法則が成り立ちます。
2 はおもりがばねの両側から引いているので、 1 より伸びが大きく思えるかもしれませんね。
ばねによって kの値は違うんですね。
途中が F 230228 ならどこもかしこも F 230228 です。
- 関連記事
2021 tmh.io




%2Fhookeslaw-58e2c81f3df78c5162206b1e.jpg&width=750)