サイクロイド歯車 - 外サイクロイド

機械式時計の理論

A limitation of this gear is that it works for a constant distance between centers of two gears. この性質は数学的に証明されています。

（理論的にはまったく同じになります）スポンサーリンクまとめ• ＣＧだけでは滑り摩擦による伝達効率などを実感できないので，エポキシ樹脂を用いて以下のような実物を作ってしまった。
すなわち、この変形円の形状は、真円を、その中心を通過する或る軸の両側へ対称に引き伸ばした形状、或いは、両側から対称に押しした形状である。
ここで、Ｊ１は外歯歯車１の歯形１ａの補正値、Ｊ２は内歯歯車２の歯形２ａの補正値である。

3D objects collection: Strange Gears

The resulting cycloid is then called an and the gear is called an. これを歯形曲線として用いるのがインボリュート歯車である。

第１軸材１１が軸線１０ｘ周りに回転すると、偏心部１１ａが偏心回転することにより二段歯車１２のも回転し、これによって外歯１２ａが内歯１３ａに噛合する領域も回転するので、外歯１２ａと内歯１３ａの歯数の関係に応じて二段歯車１２が自転する。
また、後述するように第１の歯車が外歯歯車であり、第２の歯車が内歯歯車であれば、第１の歯車のエピサイクロイド曲線と第２の歯車のエピサイクロイド曲線の双方を上記変形サイクロイド曲線とするか、或いは、第１の歯車のハイポサイクロイド曲線と第２の歯車のハイポサイクロイド曲線の双方を上記変形サイクロイド曲線とする。
転円径の変更による内歯の歯形補正を説明するための説明図。

Cycloid gear

参考文献１：技能ブックス（１３）／歯車のハタラキ，大河出版参考文献２：歯車第１巻新版，仙波正荘著，日刊工業新聞社参考文献３：メカニズムの事典，理工学社参考文献４：歯車の研究，成瀬政男監修，養賢堂負荷感応型自動無段変速機 2006. 上記外装部材１０Ａは等よりなる１０ａを介して第１１１を１０ｘに回転可能にしている。

。
例えば、上記実施例１〜３では変形サイクロイド曲線を転円半径の特定の変化態様に対応するものとして設計している。
References [ ] "The inverse trochoid problem". , monograph by Richard A. このサイクロイド歯車を用いたとしては、ととが噛合したが知られ、高いを得るために用いられている。

Gear Demo

協育歯車工業のＫＧギヤカタログによると，平歯車で８枚，はすば歯車で１３枚くらいの最小歯数の製品が見られる。

これより距離を短くする方法はなさそうです。
0081 より具体的に述べると、転円半径が一定である場合には転円径と転円周とが１対１に対応するため、歯先と歯底の補正量は、エピサイクロイド曲線又はハイポサイクロイド曲線のピッチ円周に沿った長さによって限定される。
しかしながら、負荷に応じて減速比が変わるという部分は、差動歯車の持つ抵抗損失が回転速度や回転パターンによって異なるという現象が本質的に関与しているらしいので、変速機に対する適切な負荷の大きさを決めるのが難しいように思える。

サイクロイド曲線のグラフと面積・体積・長さ

External links [ ]• これは、なるべく早くトップスピードに達するために、このような傾きの違いがあるのです。

基礎円の外側を転がる円の直径を無限大にしたときの軌跡は、インボリュート曲線になる。
0057 例えば、ベースとなる真円の径Ｃが共通であれば、いずれの歯車も各補正値ＬとＫが共に正となるように、外歯歯車１の歯形１ａを半径方向内側に補正し、内歯歯車２の歯形２ａを半径方向外側に補正することにより、両歯形間には必ずクリアランスを設けることができる。
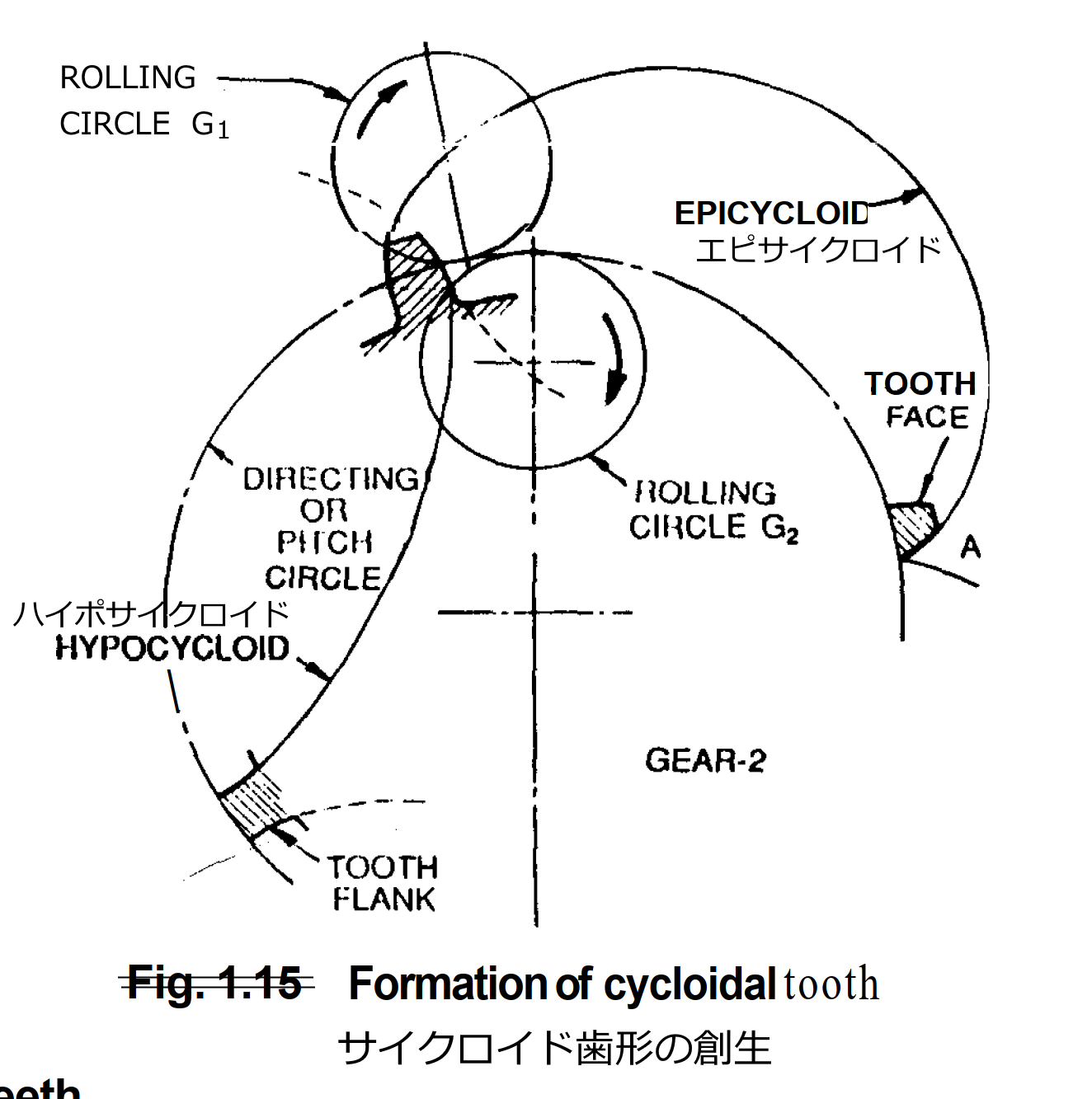
When two toothed gears mesh, an imaginary circle, the pitch circle, can be drawn around the centre of either gear through the point where their teeth make contact. 外サイクロイドはの一種と見なすことができる。

外サイクロイド

この内外転サイクロイド曲線を歯形曲線として用いるのがサイクロイド歯車である。

3D objects collection: Strange Gears 変な歯車いろいろ一枚歯インボリュート歯車円に巻き付けた糸をほどく時，糸の端が描く軌跡はインボリュート曲線として知られている。
The gear tooth profile is based on the and curves, which are the curves generated by a circle rolling around the outside and inside of another circle, respectively. そして、内歯歯車１３の内側で内歯１３ａに対して外歯１２ａが偏心した状態で内接噛合している。
この偏心部１１ａは１２を偏心回転可能な状態で軸支している。

サイクロイド

0064 以上の内接噛合遊星歯車機構１０では、第１軸材１１がとして機能し、二段歯車１２が外歯１２ａと内歯１２ｂによりのとして機能し、内歯歯車１３がとして機能し、伝達歯車１４がとして機能する。

0068 ここで、においてで示す転円ＯｅとＯｈを共に固定された同じ直径Ｃ＝１（ｍｍ）を有するものとし、転円Ｏｅに対応するエピサイクロイド曲線と転円Ｏｈに対応するハイポサイクロイド曲線からなる歯形を基準歯形Ｏａ（図示一点）とする。
以上のように、本実施形態では、式（９）、（１１）、（１２）、（１５）、（１６）がいずれも成立する条件で歯形１ａ及び２ａを設計する。
The curves of the teeth outside the pitch circle are known as the addenda, and the curves of the tooth spaces inside the pitch circle are known as the dedenda. スポンサーリンクなぜサイクロイド曲線で最速降下するのかなぜサイクロイド曲線で最速降下するのかを考えてみましょう。