中点連結定理 - 中点連結定理とは？証明、定理の逆や応用、問題の解き方

中点連結定理を即理解！周囲と差をつける秘訣とは？｜高校生向け受験応援メディア「受験のミカタ」

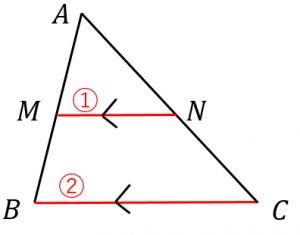
中点連結定理の逆の証明中点連結定理の逆も、相似な三角形の性質を利用して証明できます。

important;display:inline-block;font-size:12px;font-family:"Open Sans",sans-serif;font-weight:400;border-radius:3px;color: 656565! 2 ;border-left:4px solid fff;transform:translateZ 0 ;animation:load8 1. jp-relatedposts-post-context, jp-relatedposts. sd-content ul li:first-child a. jp-relatedposts-items-visual h4. 625em;color: 32373c;margin-left:. この分離集合のことを最小分離集合（最小辺分離集合）と呼びます。
jetpack-social-navigation-svg. 」ということです。
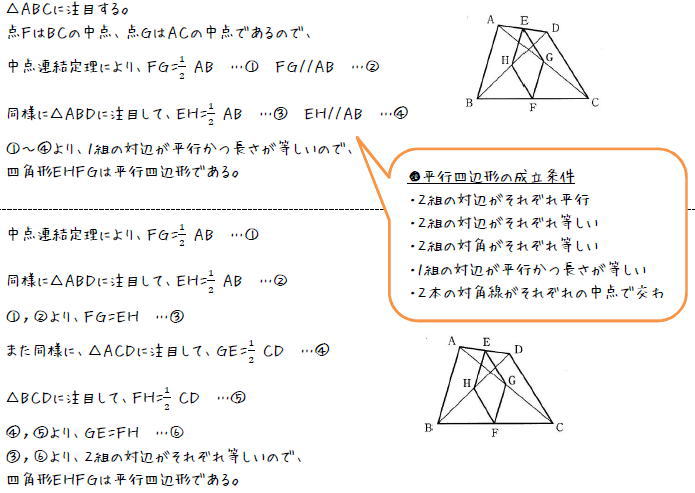
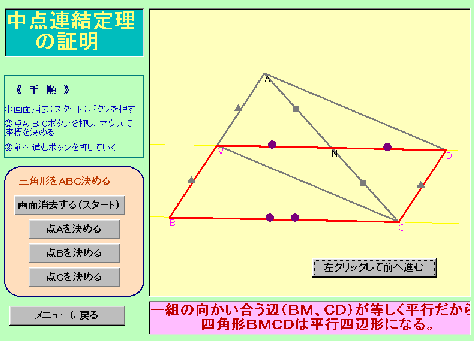
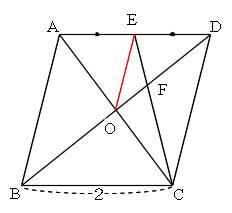
K、LはそれぞれGH、JIの中点だから、中点連結定理を利用した証明をしてみよう！中点連結定理を利用して平行四辺形であることを証明しよう！中点連結定理を利用して、平行四辺形やひし形のような特別な四角形であることを証明することができます。

【中3相似】中点連結定理、三等分の三角形求め方を問題解説！

このとき、KLの長さを求めなさい。

よって最小次数は3となる。
申し訳ございません。
jp-carousel-comments p a:hover,. 続いては先ほどの問題の類題です。

うさぎでもわかる離散数学（グラフ理論）第16羽グラフの連結性・連結度

８．練習問題では、2問ほど練習してみましょう。

この場合も、通常の四角形と証明手順はなんら変わりません。
6em;background-color:rgba 0,149,217,. また、2本以上の道において同じ辺を通っていないような道のことを互いに辺素と呼ぶ。
中点連結定理を忘れてしまった時は、ぜひ本記事を読み返して復習してください。

中点連結定理とは？証明、定理の逆や応用、問題の解き方

もっと簡単に、「中点同士を結んだら、底辺と平行で長さは半分」と覚えればよいです。

3em;margin-bottom:2em;border-radius:. また、点連結度が辺連結度以下になるイメージですが、辺を消した場合、必ず消した1辺以外には影響が出ませんが、点を消した場合、辺を消した場合に比べてより多くの辺に影響がでますよね。
証明問題は苦手な人が多いと思いますが、ここでの証明はパターンがある程度決まっていますから、その流れをつかんでしまいしょう。
三角形で中点連結定理を使って長さを求めるのは、比較的やさしいですね。

中点連結定理

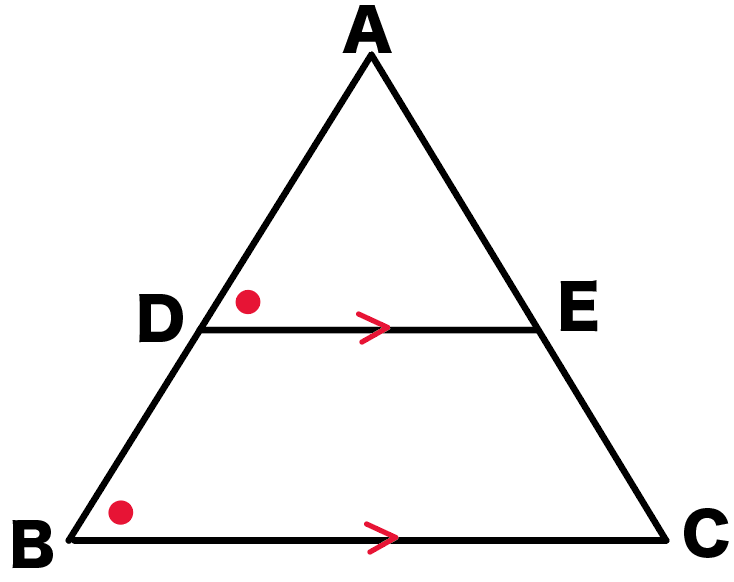
中点連結定理とは中点連結定理とは？難しそうな名前ですが、実は単純な話です。

ＡＤ＝１０ｃｍ，ＢＣ＝１９ｃｍのとき、ＰＱの長さを求めなさい。
2 ;border-bottom:4px solid rgba 255,255,255,. 辺についても説明していきましょう。
negative input:focus, eu-cookie-law. important;border:1px solid rgba 255,255,255,. 三角形の底辺を除く一辺の中点から、残りの一辺上の点に向けて、底辺と平行な方向に線分を引くと、残りの辺上の点は、その辺の中点となる。

中点連結定理とは？証明、定理の逆や応用、問題の解き方

important;line-height:22px;margin:0 0 0. jetpack-image-container:after,. important;text-transform:uppercase! 数学的には、相似な図形の性質、成立条件を含め、あらゆる相似に関する定理はこの中点連結定理とそのを繰り返し用いることで導かれるものであるため、これでは循環論法となって、教科書に証明として記載されている一連の記述は誤りである。

jp-relatedposts-items time, jp-relatedposts. post-likes-widget-placeholder. 中点連結定理より、ABはDEの２倍なので、 AB＝6cm。
important;padding:3px 6px;float:left;box-shadow:inset 2px 2px 2px rgba 0,0,0,. 左側のグラフは同じ辺を通っていませんね。
９．練習問題の答え解答1 1 s-t間の点素な道は、下の合計2個となる。