二 次 関数 最大 値 最小 値 - 二次関数の最大値/最小値の求め方(グラフや定義域が動くタイプ)
【高校数Ⅰ】二次関数最大値・最小値の基礎を元数学科が解説します。
二次関数の最大値，最小値の2通りの求め方
2次形式の最大値と最小値
二次関数の最大値，最小値の2通りの求め方
二次関数の最大値，最小値の2通りの求め方
２次関数の最小値・最大値を求めるには平方完成が鉄板！
二次関数の最大値と最小値の問題
【基本】二次関数の最大・最小（定義域に制限あり）
2次関数 : 最大値・最小値って何？「高校数学：下に凸と上に凸で異なるの巻」vol.16
１．平方完成をする。
なので、xとyの関係式を使う。
グラフを見てわかる通り、下は永遠に続いていますから。
例題： 二次関数 の最大値・最小値を求めよ。
二次関数とは？平方完成の公式や最大値・最小値、決定の問題
どうして？？と不思議に思う人に向けてくわしく説明しましょう。
この問題では定義域が指定されていないので、範囲はグラフ全域となります。
グラフが動くパターン ここから急激に面倒くさくなってきます。
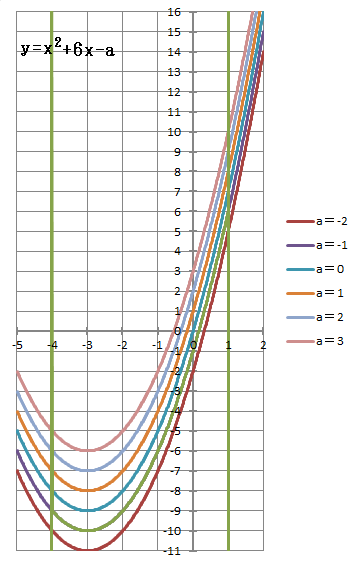
1 におけるこの関数のグラフは、下図の放物線の緑線部分です。
【二次関数】最大値と最小値を理解しよう！【実はすごく簡単です】
では、例題を通して具体的に見ていきましょう。
この公式は役に立つのでぜひ覚えておいてください。
グラフを書けば確実に理解できます。
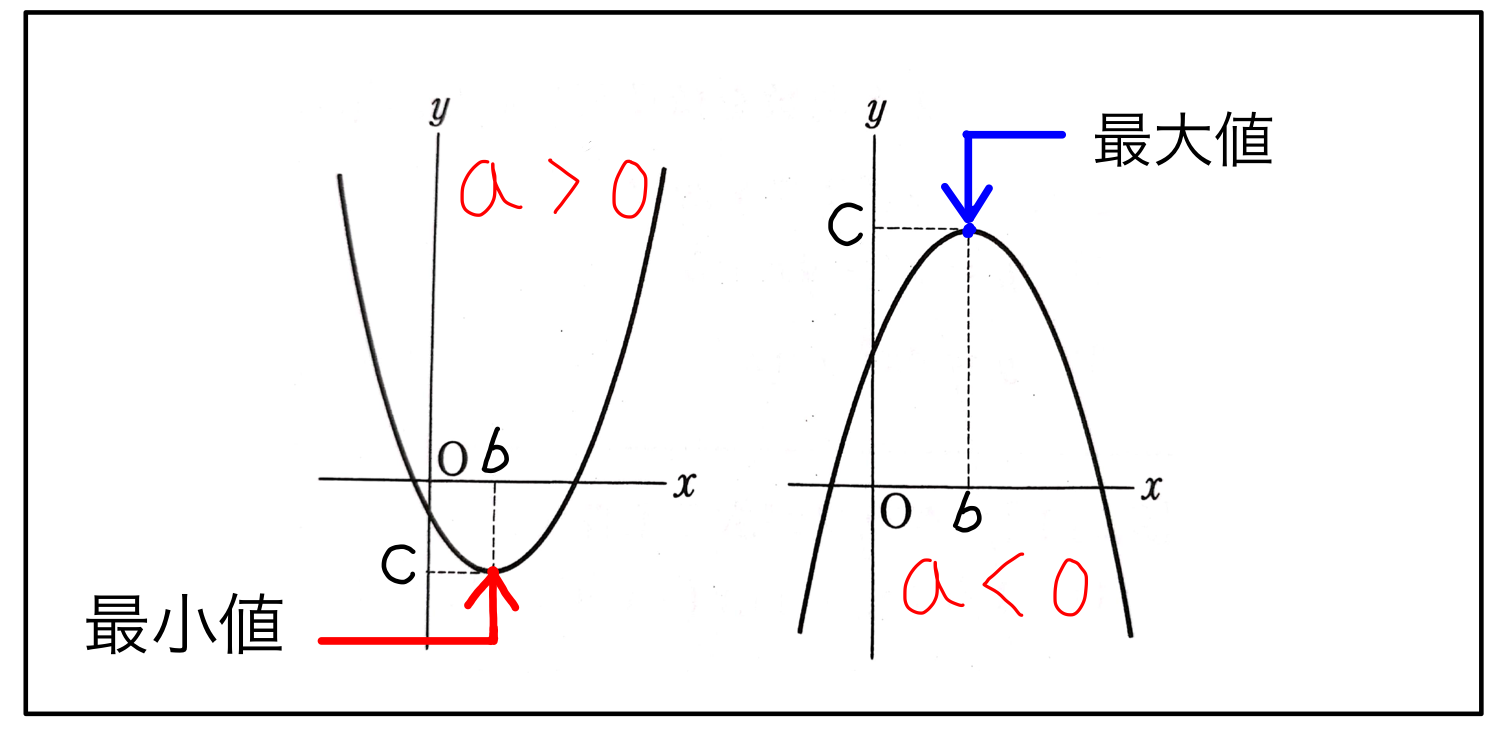
＜最大値＞ まずは最大値から考えていきましょう。
二次関数の最大値・最小値の求め方を徹底解説！｜スタディクラブ情報局
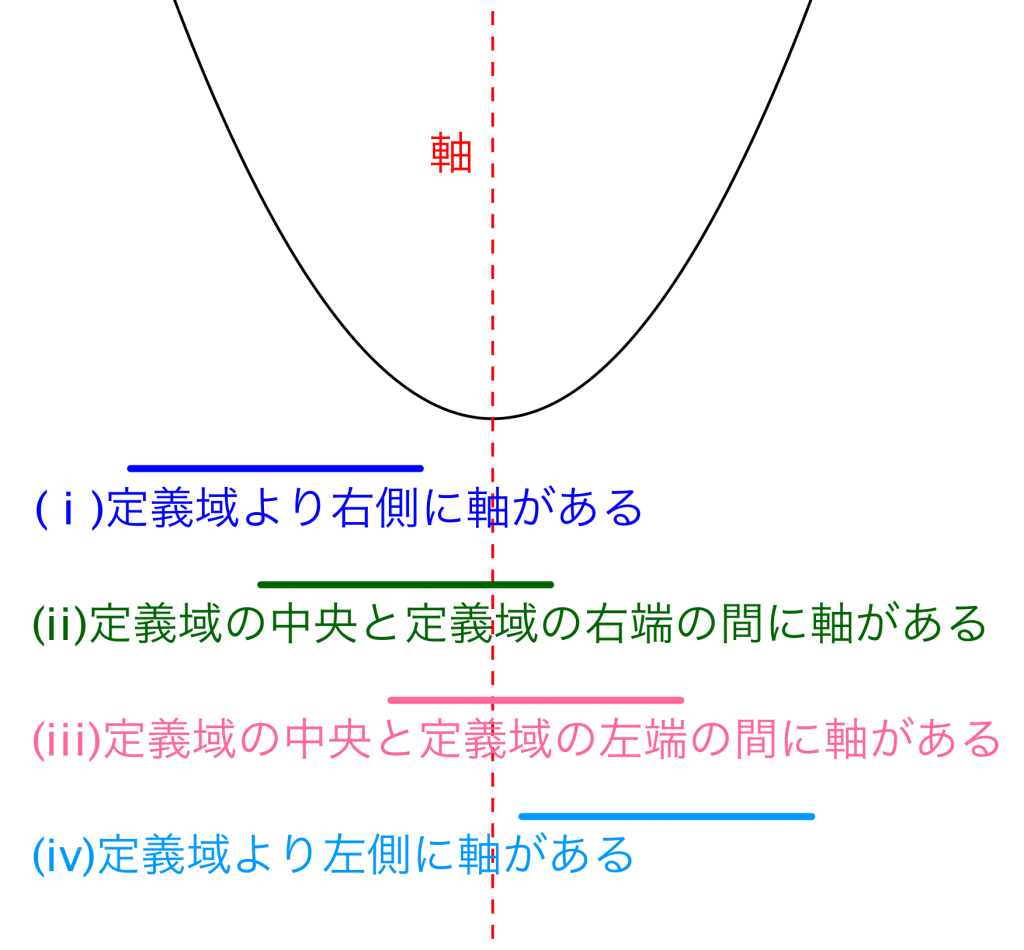
ただし、a の値によって の範囲に頂点が含まれるか否かが変わります。
少々雑だったが、ここまでがよくある書籍の解説である。
（３）最後に。
次に、変数ｘのセルを設定し、関数yのセルには関数を設定します。
二次関数の最大値/最小値の求め方(グラフや定義域が動くタイプ)
これらに注意して、問題を解いてみてください！ 関連記事. では、最大値はどうでしょうか…？ グラフを書けば一目瞭然。
」となります。
最大値は、区間の左端でとる、と思ってしまいがちですが違います。
そしてこれくらいのレベルが実際の大学入試で出されるような問題です。
二次関数の最大値・最小値の頻出問題をマスターする方法を伝授します
区間の左端ではありません。
この記事の例題を解けるようになれば、二次関数の最大値、最小値の問題で困ることはなくなります。
軸に文字を含む場合の最大値・最小値 次は、定義域ではなく関数自体（特に軸）に文字を含む場合について考えます。
二次関数の最大値最小値の求め方とは？ みなさんはもう、二次関数のグラフが書けるようになりましたね。
- 関連記事
2021 tmh.io